如果你有梦想的话,就要去捍卫它。当别人做不到的时候,他们就想要告诉你,你也不能。如果你想要些什么,就得去努力争取。就这样! – 《当幸福来敲门》
书籍链接点击 - 个人觉得可以用来入门,后面的路还很长。简要记录个人认为比较重要的内容。
数据结构绪论
数据结构:是相互之间存在一种或多种特点关系的数据元素的集合。
数据结构是一门研究非数值计算的程序设计问题中的操作对象,以及它们之间的关系和操作等相关问题的学科。
程序设计 = 数据结构 + 算法
算法
算法时间复杂度
语句的总执行次数T(n)是一个关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。时间复杂度,也就是算法的时间量度,记:T(n) = O(f(n))。
它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐进时间复杂度,简称为时间复杂度。其中f(n)是问题规模n的某个函数。
这样用大写O( )来体现算法时间复杂度记法,我们称之为大O记法。
大O记法推导:
- 1.用常数1取代运行时间中的所有加法常数。
- 2.在修改后的运行次数函数中,只保留最高阶项。
- 3.如果最高阶存在且不是1,则去除与这个项相乘的常数。得到的结果就是大O阶。
常用的时间复杂度:
- 常数阶 –
O(1) - 线性阶 –
O(n) - 对数阶 –
O(㏒n) - 平方阶 –
O(n²) - n㏒n阶 –
O(n㏒n) - 指数阶 –
O(2º)(º - n)
常用的时间复杂度所耗费的时间从小到大依次是:O(1) < O(㏒n) < O(n) < O(n㏒n) < O(n²) < O(n³) < O(2º) < O(n!) < O(nº)
O(n!):阶乘阶。
O(n):查找一个有n个随机数字数组中的某个数字。
O(㏒n):
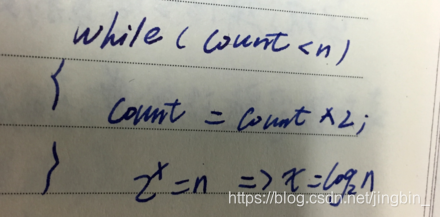
算法空间复杂度
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式记作:S(n) = O(f(n)),其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数。
小结
时间复杂度 → 运行时间的需求
空间复杂度 → 运行空间的需求
不用限定词使用“复杂度”时,通常指时间复杂度。
线性表
List:零个或多个数据元素的有限序列。(eg:幼儿园接儿子)
顺序存储结构
随着数据的插入,我们的线性表的长度开始变大,不过线性表的当前长度不能超过存储容量,即数组的长度。
线性表的长度是线性表中数据元素的个数,随着线性表插入和删除操作的进行,这个量是变化的。
线性表的长度 ≤ 数组的长度
数组 → 读取:O(1), 插入或删除:O(n)
链式存储结构
1.单链表结构:
链表: → 读取:O(n), 插入或删除:O(1)
还有:2.静态链表结构、3.循环链表、4.双向链表
栈与队列
栈:是限定仅在表尾进行插入和删除操作的线性表。
队列:是只允许在一端操作、而在另一端进行删除操作的线性表。
栈的应用
四则运算表达式求值:
后缀(逆波兰)表示法定义 -> 不需要括号"9 + (3 - 1) * 3 + 10 / 2" → "931 - 3 *+ 10 2 /+"
知道中缀表达式 → 后缀表达式
- 数字 → 输出
- 括号 → 等反括号,再输出反括号里的符号
* /→ 优先级高先出栈
总结
它们均可以用线性表的顺序存储结构来实现,但都存在着顺序存储的一些弊端,因此它们各自有各自的技巧来解决这个问题。
对于栈来说,如果是两个相同类型的栈,则可以用数组的两端作栈底的方法来让两个栈共享数据,这就可以最大化地利用数组的空间。
对于队列来说,为了避免数组插入和删除时需要移动数据,于是就引入了循环队列,是的队头和队尾可以在数组中循环变化。解决了移动数据的时间损耗,是的本来插入和删除是O(n)的时间复杂度变成了O(1)。
串
是由零个或多个字符组成的有限序列,又名叫字符串。
树(Tree)
树是n(n≥0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:
<1> 有且仅有一个特定的称为根(Root)的结点。
<2>当n > 1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2…、Tm,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
二叉树(Binary Tree)
二叉树是n(n≥0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根节点和两棵互不交换的、分别称为根节点的左子树和右子数的二叉树组成。
特殊二叉树:
1、斜树
2、满二叉树
3、完全二叉树
二叉树的存储结构
二叉树顺序存储结构
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子的关系,左右兄弟的关系等。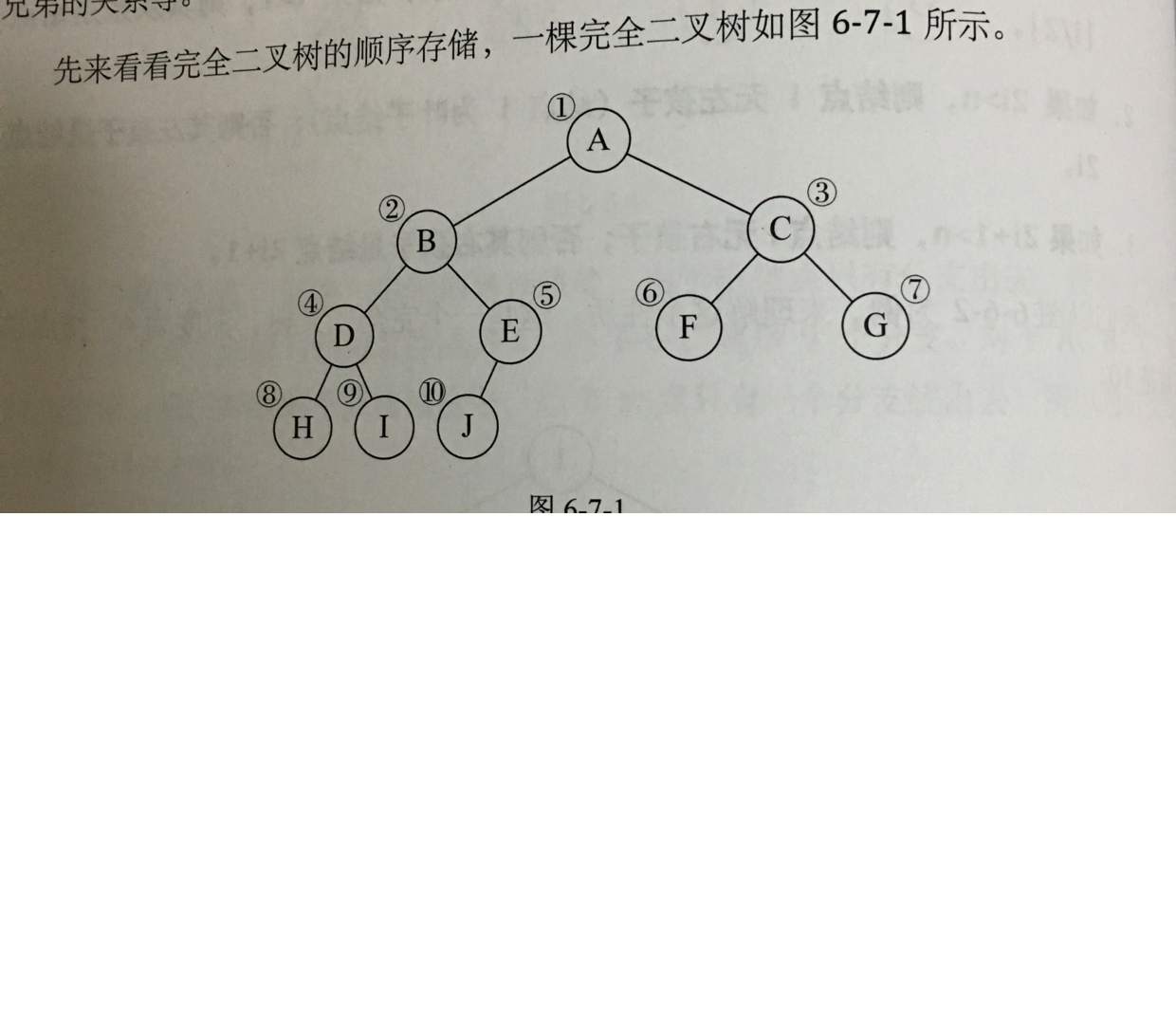
二叉链表
既然顺序存储适用性不强,我们就要考虑链式存储结构。二叉树每个结点最多有连个孩子,所以为它设计一个数据域和指针域是比较自然的想法,我们称这样的链表叫做二叉链表。
| lchild | data | rchild |
|---|---|---|
| l | A | r |
其中dataz是数据域,lchild 和 rchild 都是指针域,分别存放指向左孩子和右孩子的指针。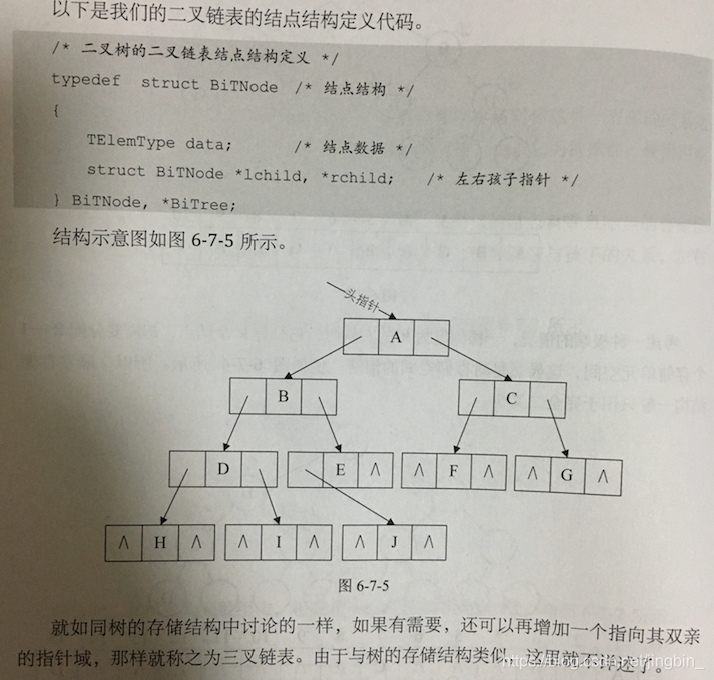
遍历二叉树
二叉树的遍历(traversing binary tree)是指从根节点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅访问一次。
遍历方法:
1、前序遍历
2、中序遍历
3、后序遍历
4、层序遍历
知道:前序:ABCDEF 中序:CBAEDF
推出:后序:CBEFDA
过程:
前序:可知[A]是根节点
中序:[CB]知道C是B的左孩子
知道:中序:ABCDEFG 后序:BDCAFGE
推出:前序:EACBDGF
过程:
后序:[E]在尾端,知[E]为根节点。
…
线索二叉树
图(Graph)
是由定点的有穷非空集合和顶点之间的集合组成,通常表示为G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
多对多的情况 → eg:人际关系
无向边:若顶点Vi到Vj之间的边没有方向,则称这条边为无向边(Edge),用无序偶对(Vi,Vj)来表示。
任意两个顶点之间的边都是无向的,则称该图为无向图。
有向边:若顶点Vi到Vj之间的边有方向,则称这条边为有向边,也称为弧(Arc)。
任意两个顶点之间的边都是有向边,则称该图为有向图。
查找
顺序查找 O(n)
有序表查找
三者的区别是:中间数取的不一样。
具有n个结点的完全二叉树的深度为[log2n]+1。→ ㏒n
二分差找 O(㏒n)
插值查找 O(㏒n)
斐波那契差找 O(㏒n)
树表查找
二叉树查找(二叉排序树)
插入和查找的时间复杂度为O(㏒n),最坏(长条)为O(n)。
优化:
平衡二叉树,为了避免上述最差的情况(O(n)),构建时,让这棵二叉排序树是平衡二叉树,此时,查找、插入和删除都是O(㏒n)。
平衡查找树之2-3查找树(2-3Tree) O(㏒n)
属于二叉树查找优化。
性质:
1、中序遍历2-3查找树,就可以得到好序的序列。
2、在一个完全平衡的2-3查找树中,根节点到每一个为空节点的距离都相同。
最坏:所有都是2-node节点,时间复杂度:㏒n
最好:所有都是3-node节点,时间复杂度:0.631㏒n
平衡查找树之红黑树(Red-Black-Tree)
2-3树实现起来比较复杂,于是有了一种简单实现的2-3树的数据结构 – 红黑树。
红黑树中将节点之间的链接分为两种不同的类型:
红色链接:用来链接两个2-nodes节点来表示一个3-nodes节点。
黑色链接:用来链接普通的2-3节点。
特性:
1、红色链接向左倾斜。
2、一个节点不可能有两个红色链接。
3、整个树完全黑色平衡。
Java:TreeMap和TreeSet都是基于红黑二叉树。
B树和B+树(B Tree/B+ Tree)
用于:文件系统和数据库系统中(硬盘里的文件)。
分块查找
哈希表查找: Map的本质是Hash表 → 以空间换时间。
key - indexed 键 - 值
时间复杂度:O(1)
排序
算法的复杂性:算法本身的复杂度,而不是指算法的时间负责度。
内排序:插入排序、交换排序、选择排序、归并排序
简单算法:
冒泡排序:O(n²)
简单选择排序:O(n²)
直接插入排序:O(n²)
改进算法:
希尔排序:O(n³/²) 不稳定
堆排序:O(n㏒n) 不稳定
归并排序:O(n㏒n) 稳定
快速排序:
冒泡排序
挨个比较,设置flag(优化)
简单选择排序
比较n次,最小交换到第1位
比较n-1次,最小交换到第2位
比较n-2次,最小交换到第3位
性能略高于冒泡排序
直接插入排序
一个记录的辅助空间,比上两种性能好一些。向前插入依次向后移动。(适用于:基本有序、少数)
希尔排序
改进的直接插入排序。
条件:基本有序(通过希尔排序达到基本有序)
将相隔某个“增量”的记录组成一个子序列,实现跳跃式的移动,使得排序的效率提高。
跳跃式的移动:导致了不稳定。
增量: increment = increment/3 + 1;
堆排序
改进的简单选择排序。
不适合排序序列较少的情况。
定义:根节点一定是堆中所有节点最大(小)值。大:大顶堆。小:小顶堆。
比较与交换跳跃式进行:导致了不稳定。
先将无序序列构建成一个堆(大顶堆),根节点为最大值,移走,将剩余的n-1重新构造成一个堆,再移走,反复执行。
重新构造:调整的是非终端结点(非叶结点)
堆排序操作的是完全二叉树(有两个子结点或无子结点),不必左小又大。
ps:平衡二叉树:高度一致,左大右小。
运行时间主要消耗在初始构建堆和在重建堆时的反复筛选上。
构建堆O(n),重建堆O(n㏒n),得到时间复杂度:O(n㏒n)。远远好于简单算法的时间复杂度。
归并排序
两两比较不跳跃(稳定)
时间复杂度:O(n㏒n),空间复杂度:O(n+㏒n)
n个有序的子序列,长度为1,两两合并,得到[n/2]。然后再两两合并….
一个无序序列,先分散我一个个单个序列,然后再合并。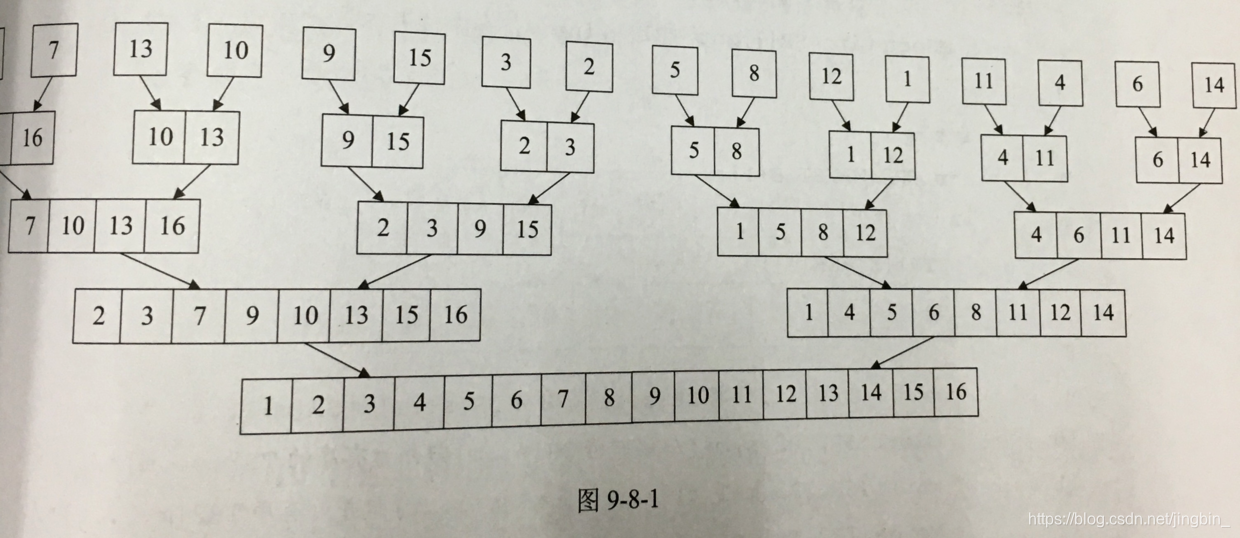
比较占用内存,但却效率高且稳定的算法
使用此算法时,尽量考虑非递归方法。
快速排序
直接插入排序的升级。不稳定
时间复杂度:
平均和最好:O(n㏒n);
最坏:O(n²);
空间复杂度:
平均和最好:O(㏒n);
最坏:O(n);
基本思想是:通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行排序,以达到有序的目的。
Partition函数:
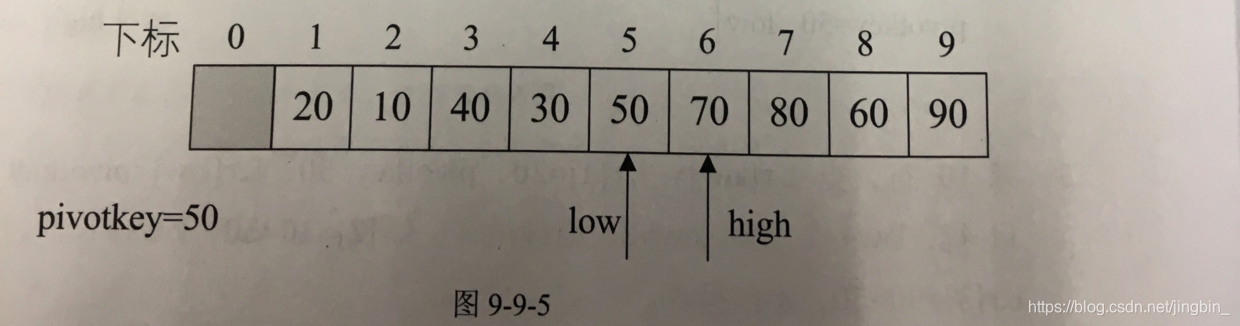
取一个关键字(pivot枢轴)。先定一个关键字,然后想尽办法让,左边的值都比它小,右边的值都比它大。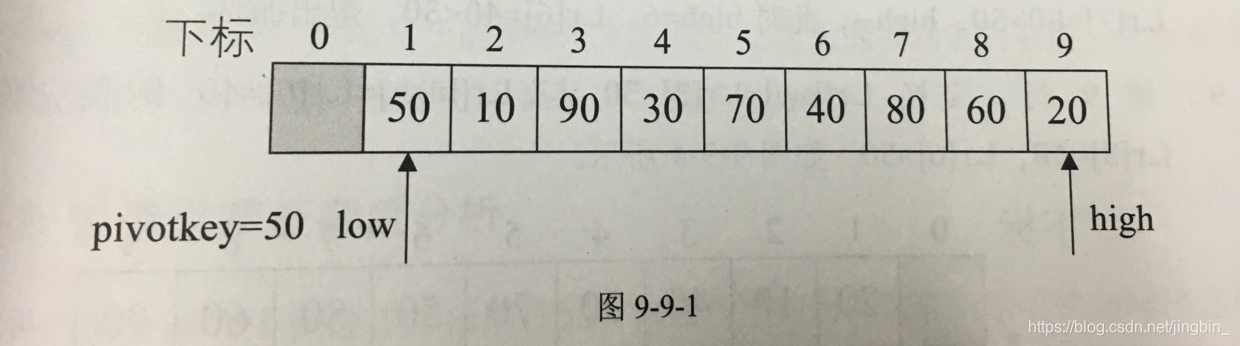
50>20 → 交换内容
交换后 20<pivotkey,low++
high里的值为50,不大于50,high不动
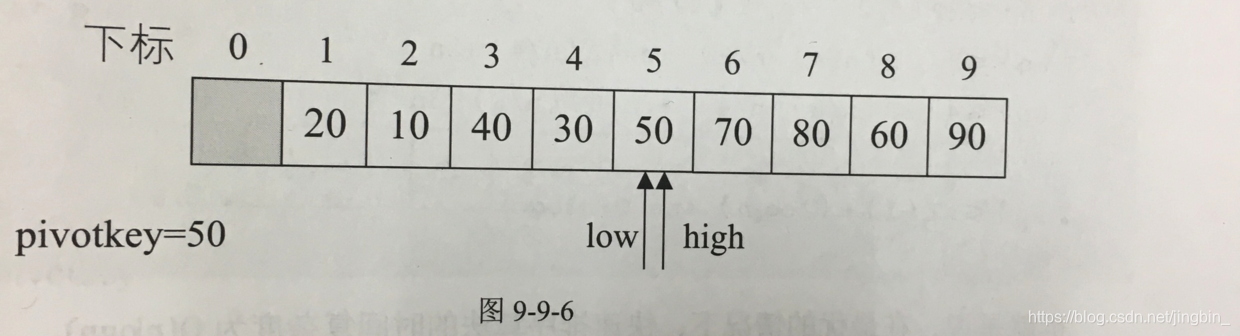
交换之后: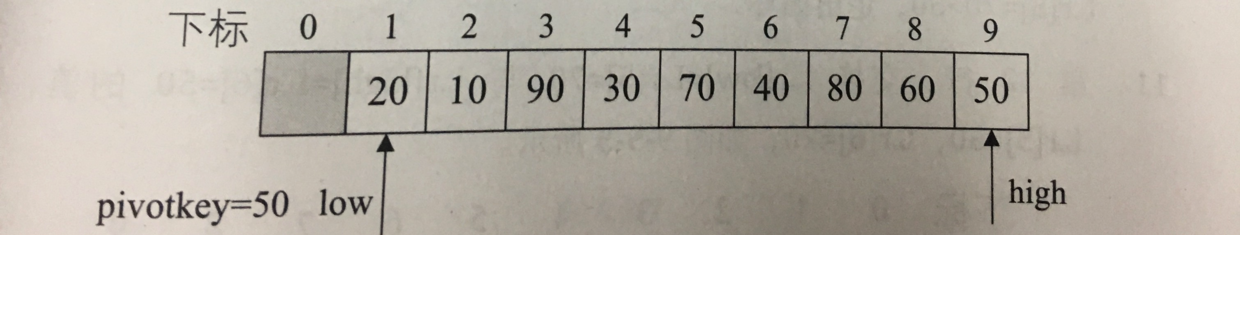
到角标为3时:
low的值为90 > high的值为50 → 交换内容
交换后 high里的值为90 > 50, → high–
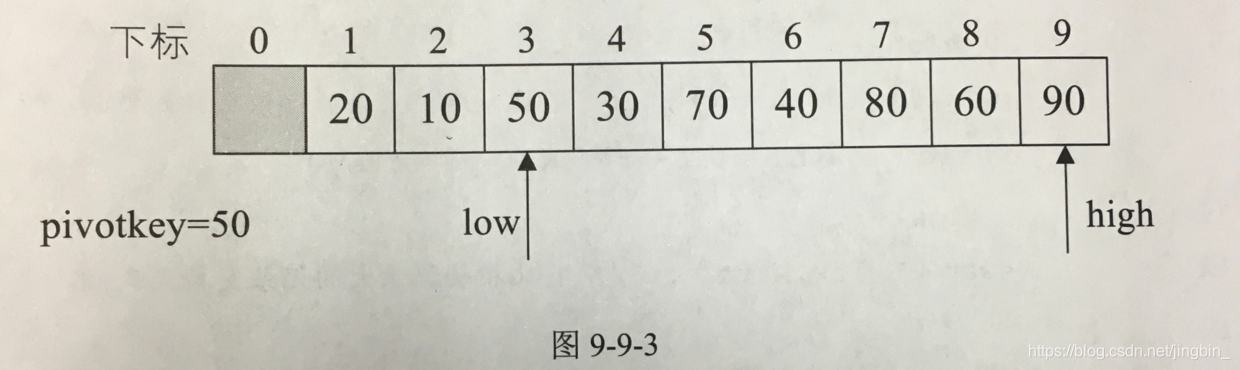
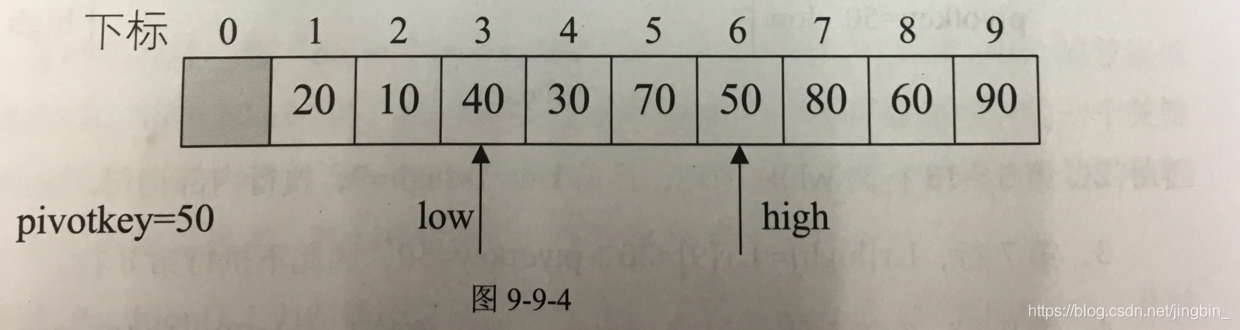
优化:
- 1、优化选取枢轴(三数取中,九数取中)
- 2、优化不必要的交换(先备份在L.r[0]中(头中),再直接替换,省掉中间交换)
- 3、优化小数组时的排序方案(如只有7个或50个,用直接插入排序,大于则快速排序)
- 4、优化递归操作(递归要时间,减少,使用尾递归)
总结
- 插入排序类:
直接插入排序
希尔排序 - 选择排序类:
简单选择排序
堆排序 - 交换排序类:
冒泡排序
快速排序 - 归并排序类:
归并排序

